Secret Santa Simulation

In December 2023, I participated in a Secret Santa event with 16 of my friends (see above). It was my first experience with a Secret Santa in such a large group. To our surprise, when we opened our gifts, my friend Jesse and I discovered that we had been assigned to each other as gift-givers. This was the only case of mutual gift exchange in our group, with no other pairs experiencing this kind of reciprocity. I was curious to know: what were the odds of this happening?

Create Intial Lineup

Below is an example of a table representing a lineup for Secret Santa.

Giver	Recipient
Walter	Bea
Nolan	Keegan
Michael	Onea
Devon	Henry
Helen	Carol
Bea	Nolan
Onea	Devon
Shelby	Helen
Keegan	Walter
Henry	Michael
Sid	Julie
Carol	Shelby
Julie	Sid
Maren	Garret
Garret	Maren
Fiona	Gus
Gus	Fiona

What we will do with this table is permute the “giver” column while leaving the “recipient” column as is. We then will count the number of times a reciprocal pair occurs and plot how frequently they occur. However, we must first address one large issue. When permuting columns, it is likely to get a lineup where someone’s name occurs twice in the same row, i.e., they give a gift to themselves. We do not want this to happen, so we must create a workaround.

Check Number of Matches in a Lineup

This code does exactly what is mentioned previously: it allows us to detect if there is a lineup where someone gives a gift to themselves.

#if this function returns anything but zero, it means there is a match, which we do not want. 
checkMatch <- function(shuffle){
  santaLength = nrow(names)
  match_count = 0
  bad_tibble_count = 0
  
  for (i in 1:santaLength){
    if(shuffle $recipient[i] != shuffle$giver_shuffle[i])
      match_count = match_count + 1
  }
  if(match_count != count(names)){
    bad_tibble_count = bad_tibble_count + 1
  }
  return(bad_tibble_count)
}

Simulate 3000 Lineups

Now we will simulate 3000 lineups and use our checkMatch() function to find those that are usable. Why 3000 lineups? I figured out ahead of time that this would give us around 1000 usable lineups due to the nature of the derangement of 17 items.

#creating list to store 1000 shuffles 

shuffled_tibbles <- list()

# place 3000 permuted tibbles in the list
for(i in 1:3000){
  shuffled_giver <- sample(names$giver)
  new_tibble <- tibble(recipient = names$recipient, giver_shuffle =shuffled_giver)
  shuffled_tibbles[[i]] <- new_tibble
}

#check how many of them have at least one match, where giver and recipient are the same person. 
how_many_bad_tibbles <- function(list){
  bad_tibbles = 0
  for(i in (1:length(shuffled_tibbles))){
  {
    if(checkMatch(shuffled_tibbles[[i]]) != 0)
      bad_tibbles = bad_tibbles + 1
  }
}
  return(bad_tibbles)
}

#check our shuffled_tibbles
how_many_bad_tibbles(shuffled_tibbles)

[1] 1903

Initial Testing Results

We can see that 1903 of our lineups had one or more instances of someone giving themselves a gift, which is nearly 2/3rds of all of our lineups.

Subset of “Good” Lineups

To make sure that we have no rows where the giver and recipient are the same person, we create this function called remove_bad_tibbles. In the end, we will have a list of “good” lineups that we will iterate over to count reciprocal pairs.

remove_bad_tibbles <- function(list){
  #initialize empty list and an index so we don't skip over indices that don't match the if statement. 
  good_tibbles <- list()
  good_tibble_index = 0 #r indexes at 1, this should work
    for(i in (1:length(shuffled_tibbles))){
  {
    if(checkMatch(list[[i]]) == 0){ 
      good_tibble_index = good_tibble_index + 1
      good_tibbles[[good_tibble_index]] <- list[[i]]
    }
    
  }
    }
    return(good_tibbles)
}

good_tibbles <- remove_bad_tibbles(shuffled_tibbles) #store results in list
length(good_tibbles) #total number of tibbles that do not have matches

[1] 1097

We can see that we have simulated 1097 lineups without any matches. For our purposes, this is enough to perform the following analysis.

Analysis of “Good” Lineups

The following function checks to see how many reciprocal pairs occur in our usable lineups. A usable lineup is a lineup where nobody gives themselves a gift.

count_reciprocal_pairs <- function(data) {
  count = 0
  
  for(i in 1:nrow(data)) {
    # We check if there's a row where the current row's giver is the recipient and vice versa. We essentially reverse the order of recipient and giver and check if that exists elsewhere. 
    reciprocal_exists <- data %>%
      filter(recipient == data$giver_shuffle[i], giver_shuffle == data$recipient[i]) %>%
      nrow() # creates a tibble of all matches for a given row of giver/recipient
    
    if(reciprocal_exists > 0) {
      count = count + 1
    }
  }
  
  # Since each pair is counted twice, we divide the count by 2 to get the unique pairs
  return(count / 2)
}

Nice! The last thing to do is to plot how frequently each reciprocal pair occurs. What I mean by this is sometimes you will have lineups with 0 reciprocal pairs, sometimes there are 1,2, etc.

Plot of Reciprocal Pairs

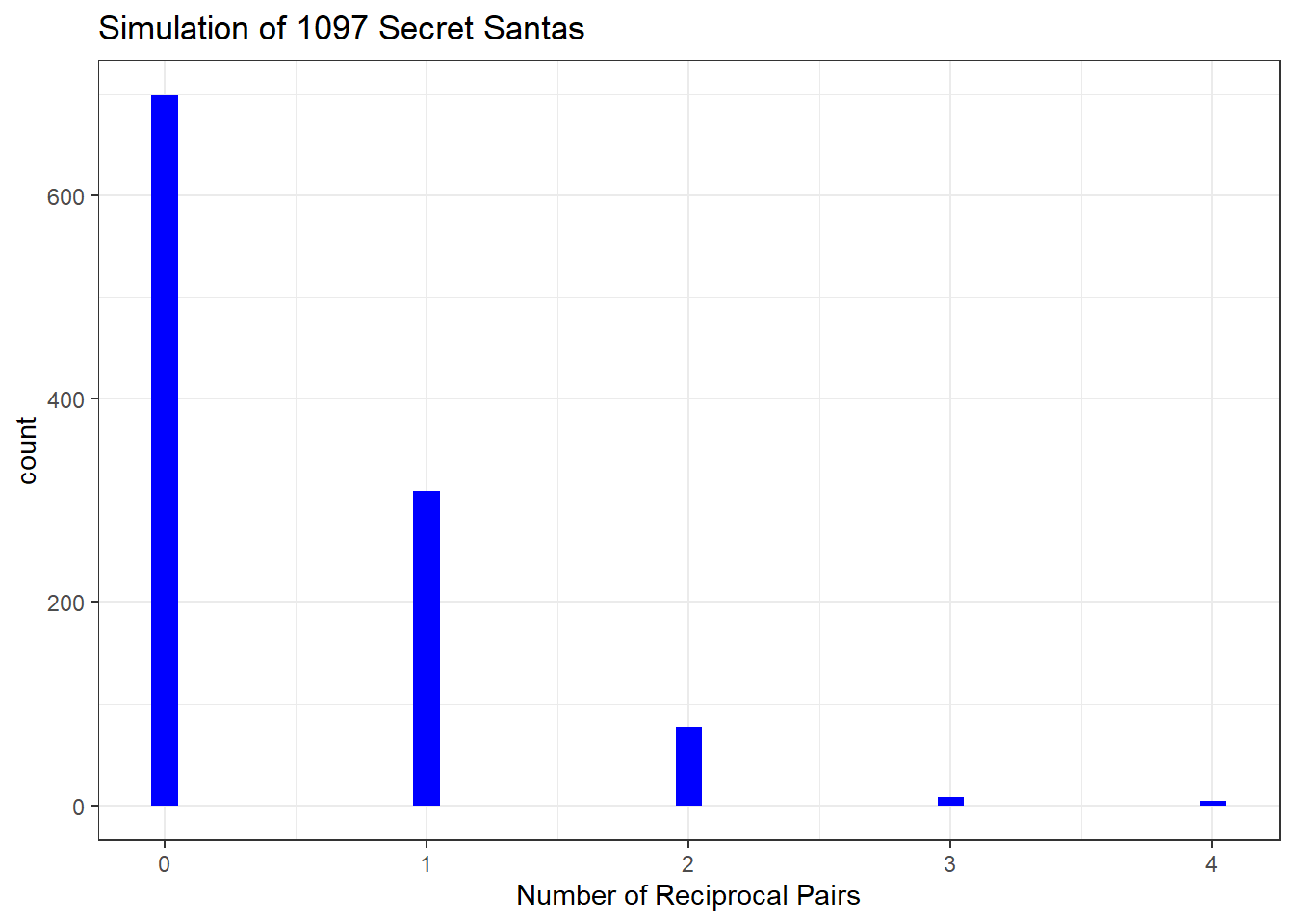
sum(pairs_vector)/length(good_tibbles)

[1] 0.4585232

In our results, about 45.9% of the time we can expect that there will be 1 or more reciprocal pairs when creating Secret Santa lineups with 17 people. That is a higher proportion than I initially expected. In the future, I would like to investigate this phenomenon with varying group sizes to see how the frequency of reciprocal pairs changes.

Link to my GitHub Code